Beth Burroughs, Chair of the Math Department at Montana State University, recently spoke to a roomful of actors and designers working for Bozeman Actors Theatre (BAT): “Don’t be afraid of math. Most people think of mathematics as dealing with a set of numbers and are scared by that. But mathematics is not about numbers, but rather it’s about ideas and thoughts.” With this admonition to the cast and crew of BAT’s upcoming production of Tom Stoppard’s Arcadia, the show got up on its feet and rehearsals began.

Why would a mathematician be talking to actors about numbers and mathematical theories? It turns out that Arcadia is a brilliantly written, award-winning piece of theatre, exploring a multitude of ideas that speak to the Classical Period as it morphs into the Romantic Period, covering themes as seemingly diverse as pursuit of knowledge, especially mathematics (including chaos theory, quantum mechanics, fractals, and Fermat’s Theorem). Further, the story includes themes of sexual hunger, order and disorder, the passage of time and how we try to reconcile ourselves to the losses that come with it. Yet, the brilliance of Stoppard’s writing ties these themes together into a wonderful comedy that leaves one pondering how we have come to be the people we are.

The Classical Period (otherwise referred to as “neo-classical” or simply “The Enlightenment”) is symbolized by things such as those perfect English gardens so neatly planned, ordered, and finely manicured; life was orderly, and a premium was placed on everything being straight-forward and black and white. Science was known to be clear, and Isaac Newton’s Laws were the gold standard. Respected philosophers of this period included John Locke, Jean-Jacques Rousseau, Immanuel Kant, Adam Smith, and Benjamin Franklin. Famous writers such as Jonathan Swift, Molière, John Dryden, Alexander Pope and Voltaire were building on the advances that had been made during the preceding Renaissance.

The Romantic Period followed the neo-classical period, and was defined by writers and philosophers who rebelled against the principled order and restraints of Classicism. Romantics placed their emphasis on emotion, rather than intellect, and strongly encouraged an individual’s free expression. Poetry thrived during this period, with Coleridge, Blake, Wordsworth, Byron and Keats known as very popular poets of that time.

Arcadia begins in 1809, set in the neo-classical period. Later in the play, the action switches to the present, influenced by Romanticism. The present-day family tries to understand their family’s history, and thus the play switches back and forth between modern day action and the older Classical Period. As the modern day characters of Hannah, Chloe, Bernard, Valentine, and Gus try to understand their family and who they are, they discover that mathematics provides the road map to discover their family’s history. 

Arcadia’s themes are presented in a series of dichotomies. Most prominent is chaos versus order. The play’s characters and action embody this, moving from a settled social order, in which relationships arise, toward the final scene, where the social order – and even the separation of the two eras – dissolves in chaos during a party; relationships collapse, and the characters die or disperse. Yet within that chaos, order can still be found. As Valentine declares: “In an ocean of ashes, islands of order. Patterns making themselves out of nothing.”

A parallel mathematical development between the two time periods using fractals and iteration takes place in Arcadia as Valentine tries to predict grouse population fluctuations over the years on the manor’s Sidley Park Estate. Curiously, he is using the exact same techniques that Thomasina (the 15 year old girl from 1809 who was a mathematical genius and the star of the Arcadia show) had experimented with years earlier.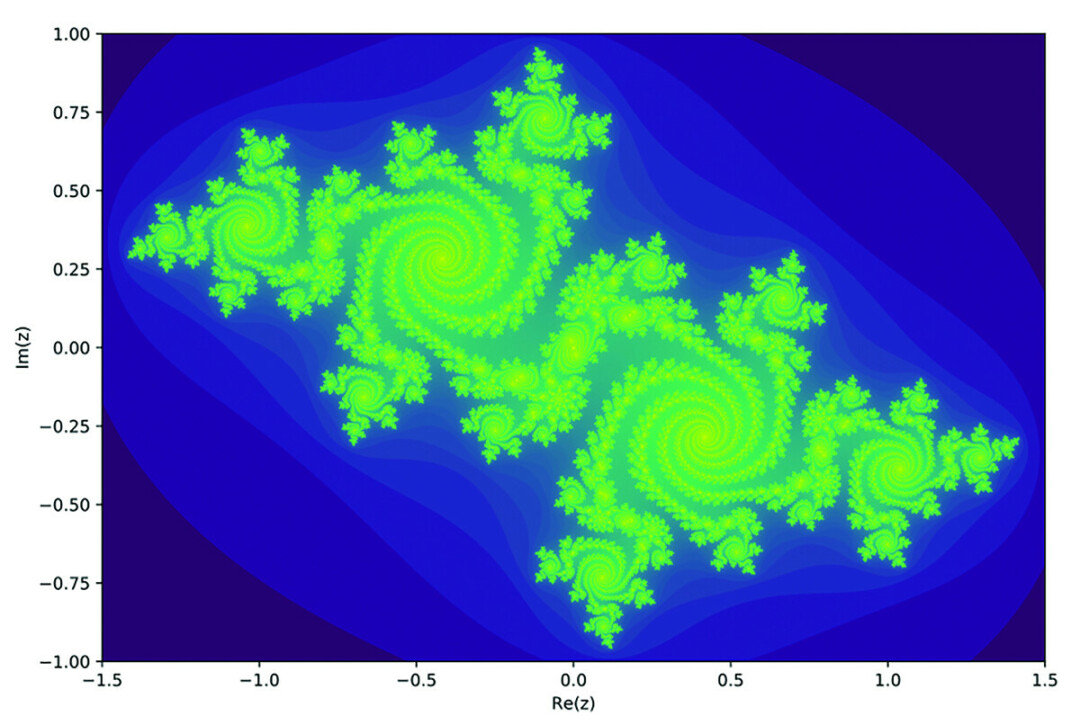

Beth Burroughs explains iteration this way; “The idea of iteration is that you specify a rule and choose a number to apply the rule to in order to generate a new number. Then you apply that rule to the new number, and to the next new number, and to the next new number, and so on. If you keep track of the numbers that are generated, you can look for patterns and ask what’s interesting about those patterns. For example, “square the number and then subtract 1.” In mathematical notation, I use x to represent my number and y to represent the number that is generated, so the rule is expressed as y = x^2 – 1. If I choose the starting number x = -1, then the first iteration has x = -1 and it generates y = 0. So in the second iteration, I use x = 0, and it generates y = -1. Then in the third iteration I’ll use x = -1 and generate y = 0. And in this case, with the rule I’ve chosen and the initial x value I’ve chosen, you can see a pattern develop, where the rule generates the value 0, then -1, then 0, then -1, and so on.

The characters in the play notice that there are lots of natural phenomena, like how a population of goldfish in a pond changes over time, that can be examined using this kind of iterative process. And the process leads to interesting patterns that lead to new questions and new mathematical ideas. (See the colorful picture accompanying this article for a visual representation of “iteration.”)

Although the play’s world grows increasingly chaotic – with overlapping time periods, increasingly complex ideas, and ever greater variations in social norms and assumptions – connections and order can still be discovered. The characters attempt to find and articulate the order they perceive in their world, even as it is continually overturned.

The development of landscape garden architecture in Britain during the 18th and 19th centuries parallels the transition from Classicism to Romanticism. The characters in the neo-Classical period of Arcadia spend an inordinate amount of time discussing the importance of well-designed and well-manicured gardens, symbolizing the restraints of the Classical era.

By the end of the play a variety of props have accumulated; if one saw them without having seen the play, they would seem completely random and unorganized. Entropy and chaos are represented by all these “random” props. But if one has seen the play, one has full information about the objects and the hidden “order” of their arrangement, brought about by the performance itself.

“It’s a great time to be alive, when everything you thought you knew turns out to be wrong,” Valentine says. Fermat’s Theorem in the play symbolizes that knowability is an impossibility. Interestingly enough, at the time that Stoppard wrote this play, Fermat’s principle had not been proven. However, only three months after the play premiered, it was, at long last, proven.

Valentine is reflecting on the changing times as new mathematical formulas and proofs are being discovered that contradict some established principles which were informed by classicism influences. Valentine’s quote seems to reflect today’s current state of affairs as well, especially with the advent of Artificial Intelligence.

The play’s end brings all these dichotomous themes together, showing that while things may appear to contradict Romanticism and Classicism, intuition and logic, thought and feeling – they can exist, paradoxically, in the same time and space. Order is found amid the chaos.

Directed by Tessa Welsch, this play features twelve actors, eight crew members, including a dialect coach and a dramaturg, and numerous volunteers to help set up and run the box office.

Bozeman Actors Theatre opens Arcadia on Friday evening, October 4, and continues the run on October 5 and 6, and October 11, 12, and 13, for a total of six shows, performed at Yellowstone Theological Institute (in the “Barn”) at 83 Rowland Rd, Bozeman. Tickets are available from the Bozeman Actors Theatre’s website, or at the door, as long as tickets are available.

For more information, visit Bozeman Actors Theatre at www.bozemanactorstheatre.org